Euclid's Axiom and Postulates

Euclid's 5 postulates

The "Elements”, Euclid's textbook, was a comprehensive compilation and explanation of all the known mathematics of his time, including the work of Pythagoras, Hippocrates, Theudius, Theaetetus and Eudoxus. In all, it contains 465 theorems and proofs, described in a clear, logical and elegant style, and using only a compass and a straight edge. Euclid reworked the mathematical concepts of his predecessors into a consistent whole, later to become known as Euclidean geometry, which is still as valid today as it was 2,300 years ago, even in higher mathematics dealing with higher dimensional spaces. It was only with the work of Bolyai, Lobachevskiand Riemann in the first half of the 19th Century that any kind of non-Euclidean geometry was even considered.

The "Elements” remained the definitive textbook on geometry and mathematics for well over two millennia, surviving the eclipse in classical learning in Europe during the Dark Ages through Arabic translations. It set, for all time, the model for mathematical argument, following logical deductions from inital assumptions in order to establish proven theorems.

Euclid's POSTULATES:

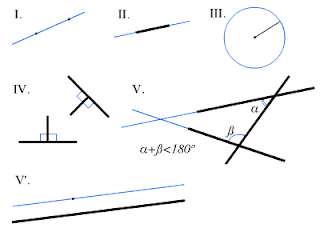
1. A straight line segment can be drawn joining any two points.

2. Any straight line segment can be extended indefinitely in a straight line.

3. Given any straight line segment, a circle can be drawn having the segment as radius and one endpoint as center.

4. All right angles are congruent.

5. If two lines are drawn which intersect a third in such a way that the sum of the inner angles on one side is less than two right angles, then the two lines inevitably must intersect each other on that side if extended far enough. This postulate is equivalent to what is known as the parallel postulate.

Euclid's fifth postulate cannot be proven as a theorem, although this was attempted by many people. Euclid himself used only the first four postulates ("absolute geometry") for the first 28 propositions of the Elements, but was forced to invoke the parallel postulate on the 29th. In 1823, Janos Bolyai and Nicolai Lobachevsky independently realized that entirely self-consistent "non-Euclidean geometries" could be created in which the parallel postulate did not hold. (Gauss had also discovered but suppressed the existence of non-Euclidean geometries.)

Euclid's AXIOMS:
1. Things which are equal to the same thing are equal to each other.
2. If equals are added to equal, the wholes (sums) are equal.
3. If equals are subracted from equals, the remainders (differences) are equal.
4. Things that coincide with one another are equal to one another.
5. The whole is greater than the part.